This week, we continues our technical series delving into the engineering/math/hardware/software aspects of module making. This week, we have part two of Tuning on the Cheap, a three-part series on how tuning works -- both in our ear and how we implement it in Eurorack. Have a technical (or non-technical) question you'd like to see addressed here? Contact us!

For part one in the series, click here.

Tuning on the Cheap: Going Digital

In the previous post, I estimated the required precision for a 1v/8va pitch voltage using Psychoacoustics. While the precision of an analog-to-digital converter (ADC) used in tuning is important, speed is of conversion (and thus the maximal sample rate) is equally so. In this post, I’ll talk about the requirements and tradeoffs between these two variables and ways around them.

The required sample rate depends on the application. For example, if a CV is being used to perform frequency modulation, then ideally we would sample it every time the output is being computed. If the CV controls something inherently latent (such as filter resonance), then we can get away with a much lower rate. The goal of today’s post is to find a reasonable sample rate for pitch signals.

Once again, we can consult the Psychoacoustic literature for some guidelines. The time it takes for our ear to detect a pitch depends on the pitch. Nineteenth-century models state that it takes the ear two cycles of a pure waveform to determine pitch but more recent work shows that this model is too strict for most pitches; we also know that the latency for us to detect pitch (in time, not cycles) is lowest around 2 kHz. We can use these numbers to determine the lowest sampling rate that will always work 2 periods at the frequency most sensitive to duration)

This rate is easy to achieve (and exceed) on almost any modern ADC.

In general, it’s best to make the sample rate as fast as possible without sacrificing precision. There are a variety of techniques that can be used to balance this tradeoff; these are particularly useful and almost always required when using lower quality / cheaper converters. Most of these techniques take the form of a low-pass filter (LPF), but there are many variations, each of which will yield slightly different results.

The first method is a simple analog LPF on the signal before the converter. The lower the bandwidth of the input signal, the lower the noise will be. Note that simple RC filters can be quite effective and cheap! Most ADCs will require a buffered signal, so a good technique is to build this filter into the buffer amplifier. Word of warning: LPFs will act as a slew and can add significant latencies to the signal!

Method two just moves this filter into the digital domain rather than analog. Implementing a simple LPF can be done easily with addition and shifts for hardware that does not have an efficient multiply.

for a simple single-pole LPF where x is the input and y is the previous output.

Another very simple technique is a window filter. Window filtering uses the average of the the last N samples. If you have more than a bit worth of noise in the signal this technique can actually give higher precision than the rated precision of the ADC! This is dependent somewhat upon the character of the noise but as long as the noise is symmetric around the signal value it will act almost as pulse-width modulation and the average will converge on the signal value. The theoretical best possible result is

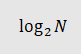
bits of additional precision when N samples are added together; in reality, you won’t get near this in any practical application, but you will generally gain some precision / reduction of noise at very little cost.

There are more advanced techniques such as outlier removal (removal of samples far from the mean) and outlier following (if a sample is far from the mean use it for the measured value else use a window filter). The first can be very useful in situations with transient noise (only occasional samples way off value) while the second is useful for situations where transient response is more important than lower noise.

One other critical point: Proper design of the buffer circuit used to drive the ADC is extremely important and needs significant attention for success. This is well documented elsewhere (e.g., here and here) but I will bring up a couple points of particular importance. ADC inputs are usually switched capacitors and will make many op amps oscillate if connected directly. An op amp stable with capacitive loads or resistance added in series between the buffer and the ADC can solve this issue. Of course, this is at odds with the fact that the driving impedance for the input needs to be as low as possible to ensure that the sampling capacitor is at the correct value after the sampling period. The exact balance to minimize noise and remove any instability will be dependent upon the buffer and ADC selected. It is imperative to measure the input to the ADC using an oscilloscope to verify that the op amp is not ringing and that the input capacitor is charging fast enough. Buffer ringing can easily move the noise floor up to -20dBFS effectively turning a 12-bit ADC into a 4-bit ADC!

Now we have digital tuning values. In the next and final installment of Tuning on the Cheap, I’ll explain how we generate a tuned pitch.

Have a technical question you'd like to see answered? New to modular and just want to know something simple? Questions about life, the universe, and everything and how it relates to modular? Submit a question for possible posting here!